TRANSFORMASI 2 DIMENSI
Setelah membaca modul ini, mahasiswa akan memiliki pengetahuan dan mampu menjelaskan (i) apa yang dimaksud dengan transformasi 2 dimensi pada objek grafik (ii) proses transformasi dasar dan melakukan proses komputasi transformasi dasar (iii) proses transformasi homogen dan mengimplementasikannya.
1 Pengertian transformasi (Fahmi Kurniawan)
Grafika komputer merupakan bidang yang menarik minat banyak orang. Salah sub bagian
dari grafika komputer adalah pemodelan objek (object modelling). Dalam pemodelan objek dua dimensi (2D), didapati berbagai objek dapat dimodelkan menurut kondisi tertentu, objek yang dimodelkan itu perlu dimodifikasi. Pemodifikasian objek ini dapat dilakukan dengan melakukan berbagai operasi fungsi atau operasi transformasi geometri. Transformasi ini dapat berupa transformasi dasar ataupun gabungan dari berbagai transformasi geometri. Contoh transformasi geometri adalah translasi, penskalaan, putaran (rotasi), balikan, shearing dan gabungan. Transformasi ini dikenal dengan transformasi affine. Pada dasarnya, transformasi ini adalah memindahkan objek tanpa merusak bentuk.
(Hasmawati)
Setelah membaca modul ini, mahasiswa akan memiliki pengetahuan dan mampu menjelaskan (i) apa yang dimaksud dengan transformasi 2 dimensi pada objek grafik (ii) proses transformasi dasar dan melakukan proses komputasi transformasi dasar (iii) proses transformasi homogen dan mengimplementasikannya.
1 Pengertian transformasi (Fahmi Kurniawan)
Grafika komputer merupakan bidang yang menarik minat banyak orang. Salah sub bagian
dari grafika komputer adalah pemodelan objek (object modelling). Dalam pemodelan objek dua dimensi (2D), didapati berbagai objek dapat dimodelkan menurut kondisi tertentu, objek yang dimodelkan itu perlu dimodifikasi. Pemodifikasian objek ini dapat dilakukan dengan melakukan berbagai operasi fungsi atau operasi transformasi geometri. Transformasi ini dapat berupa transformasi dasar ataupun gabungan dari berbagai transformasi geometri. Contoh transformasi geometri adalah translasi, penskalaan, putaran (rotasi), balikan, shearing dan gabungan. Transformasi ini dikenal dengan transformasi affine. Pada dasarnya, transformasi ini adalah memindahkan objek tanpa merusak bentuk.
Tujuan transformasi adalah :
Proses
• Merubah atau menyesuaikan komposisi pemandangan
• Memudahkan membuat objek yang simetris
• Melihat objek dari sudut pandang yang berbeda
• Memindahkan satu atau beberapa objek dari satu tempat ke tempat lain, ini biasa
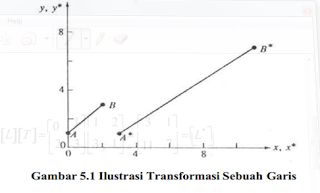
dipakai untuk animasi komputer. Transformasi dilakukan dengan mengalikan matriks objekl dengan matriks transformasi, sehingga menghasilkan matriks baru yang berisi koordinat objek hasil transformasi. Sebagai contoh, apabila sebuah garis yang melalui titik A(0,1) dan titik B(2,3)
ditransformasikan dengan matriks
maka hasilnya adalah:
Secara visual proses transformasi ini dapat dilihat pada gambar berikut:
2. Translasi
Transformasi translasi merupakan suatu operasi yang menyebabkan perpindahan objek
2D dari satu tempat ke tempat yang lain. Perubahan ini berlaku dalam arah yang sejajar dengan sumbu X dan sumbu Y . Translasi dilakukan dengan penambahan translasi pada suatu titik koordinat dengan translation vector, yaitu (tx,ty), dimana tx adalah translasi menurut sumbu x dan ty adalah translasi menurut sumbu y . Koordinat baru titik yang ditranslasi dapat diperoleh dengan menggunakan rumus :
Translasi adalah transformasi dengan bentuk yang tetap, memindahkan objek apa adanya. Setiap titik dari objek akan ditranslasikan dengan besaran yang sama. Dalam operasi translasi, setiap titik pada suatu entitas yang ditranslasi bergerak dalam jarak yang sama. Pergerakan tersebut dapat berlaku dalam arah sumbu X saja, atau dalam arah sumbu Y aja atau keduanya. Translasi juga berlaku pada garis, objek atau gabungan objek 2D yang lain. Untuk hal ini, setiap titik pada garis atau objek yang ditranslasi dalam arah x dan y masing-masing sebesar tx,ty .
Contoh
Untuk menggambarkan translasi suatu objek berupa segitiga dengan koordinat A(10,10)
B(30,10) dan C(10,30) dengan tx,ty(10,20), tentukan koordinat yang barunya !
Jawab
3.Penskalaan
Penskalaan adalah suatu operasi yang membuat suatu objek berubah ukurannya baik menjadi mengecil ataupun membesar secara seragam atau tidak seragam tergantung pada faktor penskalaan (scalling factor) yaitu (sx,sy) yang diberikan. sx adalah faktor penskalaan menurut sumbu x dan sy faktor penskalaan menurut sumbu y . Koordinat baru diperoleh dengan
Nilai lebih dari 1
menyebabkan objek diperbesar, sebaliknya bila nilai lebih kecil dari 1, maka
objek akan diperkecil. Bila (sx,sy) mempunyai nilai yang sama, maka skala
disebut dengan uniform scaling.
Contoh
A(10,10) Untuk
menggambarkan skala suatu objek berupa segitiga dengan koordinat B(30,10) dan
C(10,30) dengan (sx,sy) (3,2), tentukan koordinat yang barunya!
Jawab:
4.Rotasi
Putaran adalah suatu operasi yang
menyebabkan objek bergerak berputar pada titik pusat
atau pada sumbu putar yang dipilih berdasarkan sudut
putaran tertentu. Untuk melakukan rotasi diperlukan sudut rotasi dan pivot
point (xp,yp) dimana objek akan dirotasi. Putaran biasa dilakukan pada satu
titik terhadap sesuatu sumbu tertentu misalnya sumbu x, sumbu y atau garis
tertentu yang sejajar dengan sembarang sumbu tersebut. Titik acuan putaran
dapat sembarang baik di titik pusat atau pada titik yang lain. Aturan dalam
geometri, jika putaran dilakukan searah jarum jam, maka nilai sudutnya adalah
negatif. Sebaliknya, jika dilakukan berlawanan arah dengan arah jarum jam nilai
sudutnya adalah positif.
Contoh 1. Diketahui koordinat titik yang
membentuk segitiga {(3, -1), (4, 1), (2, 1).
Gambarkan objek tersebut kemudian gambarkan pula
objek baru yang merupakan
transformasi rotasi objek lama sebesar 90° CCW
dengan pusat rotasi (0,0).
Penyelesaian :
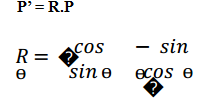
Matriks transformasi umum adalah
Rotasi dapat dinyatakan dengan :
sedangkan diketahui
lakukan subtitusi, maka :
Matriks rotasi dinyatakan dengan :
Rotasi suatu titik terhadap pivot point (xp,yp) :
Contoh 1. Diketahui koordinat titik yang membentuk
segitiga {(3, -1), (4, 1), (2, 1).
Gambarkan objek tersebut kemudian gambarkan pula
objek baru yang merupakan
transformasi rotasi objek lama sebesar 90° CCW
dengan pusat rotasi (0,0).
Jawab:
Matriks transformasi umum adalah
Maka dengan mengalikan titik-titik segitiga tersebut
dengan matriks transformasi
sesuai, maka akan diperoleh hasil yang digambarkan
sebagai berikut:
Contoh 2. Untuk menggambarkan rotasi suatu objek
berupa segitiga dengan koordinat
A(10,10), B(30,10) dan C(10,30) dengan sudut rotasi
300° terhadap titik pusat cartesian
(10,10), dilakukan dengan menghitung koordinat hasil
rotasi tiap titik satu demi satu.
Jawab:
Titik
A
x’= xp+(x - xp) cos ɵ -
(y - yp) sin ɵ
=10+(10-10)*0.9 – (10-10)*0.5 = 10
y’= yp+(x - xp) sin ɵ +
(y - yp) cos ɵ
= 10+(10-10)*0.5 – (10-10)*0.9 = 10
Titik A’(10,10)
Titik B
x’= xp+(x - xp) cos ɵ -
(y - yp) sin ɵ
=10+(30-10)*0.9 – (10-10)*0.5 = 28
y’= yp+(x - xp) sin ɵ +
(y - yp) cos ɵ
= 10+(30-10)*0.5 – (10-10)*0.9 = 20
Titik B’(28,20)
Titik C
x’= xp+(x - xp) cos ɵ - (y -
yp) sin ɵ
=10+(10-10)*0.9 – (30-10)*0.5 = 0
y’= yp+(x - xp) sin ɵ +
(y - yp) cos ɵ
= 10+(10-10)*0.5 – (30-10)*0.9 = 28
Titik C’(0,28)
5. Refleksi (Hasmawati)
Refleksi adalah transformasi yang membuat mirror
(pencerminan) dari image suatu objek.
Image mirror untuk refleksi 2D dibuat relatif
terhadap sumbu dari refleksi dengan memutar
180o terhadap refleksi. Sumbu refleksi dapat dipilih
pada bidang x,y . Refleksi terhadap garis
y=0, yaitu sumbu x dinyatakan dengan matriks
Transformasi membuat nilai x sama tetapi membalikan
nilai y berlawanan dengan
posisi koordinat. Langkah :
• Objek diangkat
• Putar 180o terhadap sumbu x dalam 3D
• Letakkan pada bidang x,y dengan posisi berlawanan
• Refleksi terhadap sumbu y membalikan koordinat
dengan nilai y tetap.
Refleksi terhadap sumbu x dan y sekaligus dilakukan
dengan refleksi pada sumbu x terlebih dahulu, hasilnya kemudia direfleksi
terhadap sumbu y. Transformasi ini dinyatakan dengan :
Refleksi ini sama dengan rotasi 180° pada bidang xy
dengan koordinat menggunakan titik pusat koordinat sebagai pivot point.
Refleksi suatu objek terhadap garis y=x dinyatakan dengan bentuk matriks.
Ilustrasi proses refleksi pada sumbu-sumbu utama digambarkan pada gambar berikut:
Matriks dapat diturunkan dengan menggabungkan suatu
sekuen rotasi dari sumbu
koordinat merefleksi matriks. Pertama-tama dilakukan
rotasi searah jarum jam dengan sudut
45° yang memutar garis y=x terhadap sumbu x.
Kemudian objek direfleksi terhadap sumbu y,
setelah itu objek dan garis y=x dirotasi kembali ke
arah posisi semula berlawanan arah
dengan jarum jam dengan sudut rotasi 90°.
Untuk mendapatkan refleksi terhadap garis y=-x dapat
dilakukan dengan tahap :
• Rotasi 45° searah jarum jam
• Refleksi terhadap axis y
• Rotasi 90° berlawanan arah dengan jarum jam
Dinyatakan dengan bentuk matriks
Refleksi terhadap garis y=mx+b pada bidang xy
merupakan kombinasi transformasi
translasi – rotasi – refleksi .
• Lakukan translasi mencapai titik perpotongan
koordinat
• Rotasi ke salah satu sumbu
• Refleksi objek menurut sumbu tersebut
Latihan
Diketahui sebuah objek dengan pasangan koordinat
{(4,1), (5,2), (4,3)}.
a. Refleksikan pada cermin yang terletak pada sumbu x
b. Refleksikan pada garis y=-x.
6.Shear
(Ely
wasiati)
Shear adalah bentuk transformasi yang membuat
distorsi dari bentuk suatu objek, seperti
menggeser sisi tertentu. Terdapat dua macam shear
yaitu shear terhadap sumbu x dan shear
terhadap sumbu y .
Shear terhadap
sumbu x
Dengan koordinat transformasi
x’= x + shx.y y’=y
Parameter shx dinyatakan dengan sembarang bilangan.
Posisi kemudian digeser menurut
arah horizontal.
Shear terhadap sumbu y
Dengan koordinat transformasi
x’=x y’=
shy.x+y
Parameter shy dinyatakan dengan sembarang bilangan. Posisi koordinat
kemudian menurut
arah vertikal.
Gambar di bawah mengilustrasikan proses shearing.
Latihan
Diketahui sebuah bidang segiempat dengan koordinat
A(3,1), B(10,1), C(3,5) dan
D(10,5). Tentukan koordinat baru dari bidang
tersebut dengan melakukan translasi dengan
faktor translasi (4,3)
1. Lakukan penskalaan dengan faktor skala (3,2)
2. Dari hasil (1) lakukan rotasi terhadap titik
pusat (A) dengan sudut rotasi 30o.
3. Transformasi shear dengan nilai shx = 2 dengan
koordinat A(0,0), B(1,0), C(1,1), dan
D(0,1)
4. Transformasi shear dengan nilai shy = 2 dengan
koordinat A(0,0), B(1,0), C(1,1), dan
D(0,1)
7. Transformasi Homogen (Arjuna
Wirapanji)
Transformasi homogen merupakan transformasi yang
memberikan cakupan proses
transformasi secara umum. Dalam dunia nyata dimana
objek nyata merupakan elemen yang
kompleks dan memiliki koordinat masing-masing, maka
peran transformasi homogen sangat
diperlukan untuk menyelesaikan berbagai permasalahan
yang ada.
Beberapa hal yang perlu diperhatikan dalam hal
implemengtasi transformasi homogen
adalah sebagai berikut:
• Origin bersifat INVARIAN. Koordinatnya tidak akan
pernah berubah. Jika
ditransformasikan, akan tetap di (0,0).
• Dalam kondisi nyata, origin tidak harus selalu
absolut di (0,0). Untuk itu
digunakan koordinat homogen
• Koordinat homogen memetakan titik (0,0) ke posisi
lain. Untuk itu ada elemen
tambahan pada
matriks transformasi
Untuk itu maka didefinisikan Matriks Transformasi
Umum (MTU) sebagai berikut:
Dimana a, b, c, d merupakan elemen untuk skala,
rotasi,refleksi dan shearing; m, n
merupakan elemen untuk translasi; s adalah elemen
untuk overal scaling; dan p, q adalah
elemen untuk proyeksi.
Rotasi
pada Sumbu Sembarang
Jika sebuah objek dirotasikan sebesar θ° dengan
pusat rotasi (m, n), maka langkahlangkah yang
harus dilakukan adalah
a. Translasikan pusat rotasi ke (0, 0); karena yang
kita ketahui hanyalah rumus rotasi
pada origin
b. Lakukan rotasi sebesar yang diinginkan
c. Re-translasi pusat rotasi ke posisi semula
Dengan demikian matriks transformasinya menjadi
• Origin bersifat INVARIAN. Koordinatnya tidak akan
pernah berubah. Jika
ditransformasikan, akan tetap di (0,0).
• Dalam kondisi nyata, origin tidak harus selalu
absolut di (0,0). Untuk itu
digunakan koordinat homogen
• Koordinat homogen memetakan titik (0,0) ke posisi
lain. Untuk itu ada elemen
tambahan pada
matriks transformasi
Untuk itu maka didefinisikan Matriks Transformasi
Umum (MTU) sebagai berikut:
Dimana a, b, c, d merupakan elemen untuk skala,
rotasi,refleksi dan shearing; m, n
merupakan elemen untuk translasi; s adalah elemen
untuk overal scaling; dan p, q adalah
elemen untuk proyeksi.
Rotasi
pada Sumbu Sembarang
Jika sebuah objek dirotasikan sebesar θ° dengan
pusat rotasi (m, n), maka langkahlangkah yang
harus dilakukan adalah
a. Translasikan pusat rotasi ke (0, 0); karena yang
kita ketahui hanyalah rumus rotasi
pada origin
b. Lakukan rotasi sebesar yang diinginkan
c. Re-translasi pusat rotasi ke posisi semula
Dengan demikian matriks transformasinya menjadi:
Proses ini diilustrasikan sebagai berikut:
Refleksi pada Garis Sembarang
Jika sebuah objek direfleksikan pada sebuah garis maka langkah-langkah yang harus
dilakukan adalah
a. Translasikan cermin sedemikian rupa sehingga menyentuh titik origin
b. Rotasikan cermin sehingga berimpit dengan salah satu sumbu utama
c. Refleksikan objek
d. Re-rotasi
e. Re-translasi
Jadi MTU terdiri dari 5 buat matriks transformasi sebagai berikut:
Latihan:
1).Diketahui sebuah objek dengan koordinat
a. Rotasikan objek sebesar 45º CCW dengan pusat rotasi pada (9, 4)
b. Rotasikan objek sebesar 30º CW dengan pusat rotasi pada (-3,5)
Dari operasi transformasi
1. Gambarkan objek asli
2. Tentukan MTU
3. Tentukan Koordinat Objek Baru
4. Gambarkan objek hasil transformasi
2). Diketahui sebuah objek dengan koordinat
a. Refleksikan objek di atas pada cermin yang berimpit dengan garis y = –x+9.
b. Refleksikan objek di atas pada cermin yang berimpit dengan garis y = x+9.
Dari operasi transformasi
1. Gambarkan objek asli
2. Tentukan MTU
3. Tentukan Koordinat Objek Baru
4. Gambarkan objek baru hasil transformasi
Jawaban
1.a
1.b
(Fahmi Kurniawan)
2.a
2.b
(Arjuna Wirapanji)
(Hasmawati)
(Ely wasiati)
Kelompok 2
-Arjuna Wirapanji
-Ely Wasiati
-Fahmi Kurniawan
-Hasmawati











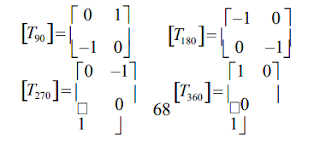
























Komentar
Posting Komentar